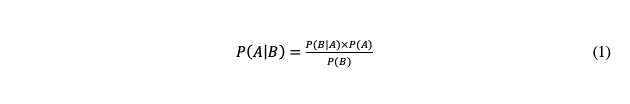Bayesian Reasoning: Navigation through Uncertain Decisions
Bayesian Reasoning: What is it and how can it help our decision-making?
By Stephanie Lo and Lucy Cui
From common tasks, like picking strawberry or chocolate ice cream, to substantial responsibilities, such as deciding which stocks to buy and sell; decision-making is a crucial aspect of our lives. Yet due to our uncertainty and lack of foresight regarding future events (Knight, 1921), making a choice can be a nerve-wracking process for many, eventually leading to more anxiety (Grupe & Nitschke, 2013).
Evolution-wise, decision-making is vital to increasing the odds of survival. Prior experiences and information are used to help predict the future and increase the chances of one’s desired outcomes, while also avoiding potential threats (Trimmer et al., 2011). However, when uncertainty arises, one’s clarity in planning and decision-making decreases, thus contributing to anxiety and stress.
Although it may be unrealistic to believe that this process can be completely anxiety-free, perhaps Bayesian reasoning – a method of statistical inference – can be used to logically navigate through it. Bayesian reasoning (or Bayesian inference) is an application of inductive reasoning – how true a statement or hypothesis is – and uses the interpretation of probability to express the world’s uncertainty. It is based on Bayes’ theorem:
is the probability of event A occurring, given event B has occurred; is the probability of event B occurring, given event A has occurred; is the probability of event A; and is the probability of event B.
Essentially, Bayes’ theorem is a probabilistic model which essentially states that the probabilities of both prior and new knowledge are needed to conclusively assess if something is true or not. Thus, the goal of Bayesian reasoning is to “rationally update” one’s beliefs, hypotheses, or views with the arrival of new evidence and/or the retrieval of old evidence (Anderson, 2000).
This idea is nothing new. It was used to crack the Enigma code during World War II; it sorts the spam in our email accounts (McGrayne, 2011); and it is helping to predict the future reproductive impact of the COVID-19 virus (Donnat & Holmes, 2021). Its various uses across different time periods and fields highlight its importance, as well as its potential application for everyday decision-making.
For situations of uncertainty in decision-making, Gleason and Harris (2019) propose that, by using what they refer to as “Bayesian updating”, one can commit to an initial decision or belief, yet also remain “flexible” on one’s choices when acquiring new information. As such, by using this method of “updating” and flexibility, one could possibly avoid the anxiety of indecisiveness, as one critically and logically considers evidence from all sides in order to confidently make a decision.
There is evidence of its helpfulness in making optimal decisions. McCann (2020) found that managers who adopted a Bayesian perspective could improve the accuracy of their estimates of the future, as well as foster “open-mindedness” and reduce cognitive bias, all of which help to promote better decision-making. Additionally, some animals, such as female fish and lekking birds, use Bayesian decision-making in order to choose the best mate, utilizing both their individual assessment of the males and the observation of other females’ choices (Uehara et al., 2005). Overall, this not only highlights Bayesian reasoning’s versatility and evolutionary characteristics once again, but also its optimization in one’s decisions.
However, there are some barriers to the application of Bayesian reasoning, namely that probabilities, for many, can be unintuitive. For example, when asked scenarios involving probability (e.g. “Imagine that we roll a fair, 6-sided die 1000 times. Of 1000 rolls, how many times do you think the die will come up even [2, 4, or 6]?”), only about 64.5% of participants from both more- and less-educated backgrounds answered correctly (Galesic & Garcia-Retamero, 2010).
Further, this misunderstanding of probabilities can lead to much more consequential effects, particularly when it comes to physician diagnoses. In a study examining breast cancer diagnoses after receiving a mammogram, 22% of women aged 40-59 were found to be over-diagnosed for breast cancer (Miller et al., 2014). Thus, although the screening test correctly identifies 90% of women with breast cancer and 90% of women without, there are many more false-positive tests than true-positive ones (Spiegelhalter et al., 2011). In fact, out of 108 positive tests, only 9 (or 8%) would be expected to truly reveal breast cancer (Spiegelhalter et al., 2011). Because of these over-diagnoses, many more women may undergo intensive measures (e.g. surgery, chemotherapy, and radiation) than need be. Yet by knowing how to incorporate the statistics of breast cancer prevalence and false-positive rate, doctors can instead better treat women with positive tests.
Perhaps this lack of Bayesian understanding is due to an inability to create mental models of the presented situations; thus, having appropriate visual representations of Bayesian problems could be used to improve reasoning. Some evidence has found this to be true. In one study, participants presented with information in frequency-type formats (e.g. 1 out of 100) solved Bayesian problems with approximately 50% accuracy, while participants using probability-type formats solved them with about 22% accuracy (Gigerenzer & Hoffrage, 1995). Additionally, graphical representations (e.g. probability maps, detection bars, contingency tables, pictographs, etc.) were found to increase accuracy and speed when solving Bayesian problems (e.g. Cole & Davidson, 1989; Brase, 2014).
Additionally, learning Bayesian reasoning can also increase one’s understanding of it. Kurzenhäuser and Hoffrage (2002) found that medical students who were taught how to translate probability information into natural frequencies using visual aids were three times more accurate at Bayesian tasks compared to those who only learned how to insert the probabilities into Bayes’ theorem. Thus, by giving people tools and training that support understanding of Bayesian reasoning, they are equipped to not only solve these kinds of problems, but to also make more precise and accurate decisions.
As with Kurzenhäuser and Hoffrage’s (2002) study, perhaps a combination of both models and learning are needed in order to best understand Bayesian inference. Take, for instance, this Bayesian problem:
15 out of 10,000 women are pregnant with a child who has Down’s syndrome. Out of these 15 women, 12 will receive a positive result from the ultrasound test on nuchal translucency. Out of the 9,985 women who are pregnant with a child that does not have Down’s syndrome, 799 will receive a positive ultrasound test. Imagine a new sample of pregnant women who receive a positive result in the ultrasound test: How many are actually pregnant with a child who has Down’s syndrome? (p. 6)
Using solely the formula of Bayes’ Theorem, the problem seems challenging to understand, let alone solve. What do these probabilities mean and where should they be inserted into this formula (Figure 1)?
To most people, this formula would probably be confusing and easily misunderstood – something that was witnessed in the study, with only 1-3 percent of participants guessing the correct solution (Kurzenhäuser & Hoffrage, 2002). However, by learning to translate this medium into a simpler and more meaningful format, it can become much easier to understand and solve a Bayesian problem.
Kurzenhäuser and Hoffrage’s (2002) translation procedure was as follows:
1. Select a population (e.g., 10,000 people) and use the base rate to determine how many of the population have the disease (in the case of Down’s syndrome, 0.15% of 10,000 unborn children is 15 children).
2. Take that result (15 children) and use the test’s sensitivity to determine how many have both the disease and a positive test (80% of 15 is 12 children).
3. Take the remaining number of people who do not have the disease (9,985 children) and use the test’s false positive rate to determine how many do not have the disease, but still test positive (8% of 9,985 is about 799 children).
4. Compare the number obtained in Step 2 with the sum of those obtained in Steps 2 and 3 to determine how many people with a positive test actually have the disease (12 out of 811 children). (p. 10)
Figure 1. Two possible methods to solving the Bayesian problem (i.e. formula versus tree diagram). In contrast to the confusing probability-format, the combined natural frequency-format and visualization can help to clarify the problem. Reproduced from Kurzenhäuser & Hoffrage (2002).
At its core, Bayesian reasoning is about probability, something that affects and governs many aspects of daily and occupational life. Furthermore, its flexible approach to our beliefs through the understanding of both prior and future information’s malleability has direct applications for decision-making, especially with the uncertainty of everyday life. Through a Bayesian perspective, we can perhaps realize and regain some control over our decisions, and maybe, this can give us some form of comfort for the future.
References
Brase, G. L. (2014). The power of representation and interpretation: Doubling statistical reasoning performance with icons and frequentist interpretations of ambiguous numbers. Journal of Cognitive Psychology, 26(1), 81–97. https://doi.org/10.1080/20445911.2013.861840
Cole, W. G., & Davidson, J. E. (1989). Graphic Representation Can Lead To Fast and Accurate Bayesian Reasoning. Proceedings of the Annual Symposium on Computer Application in Medical Care, 227–231.
Corfield, D., & Schreiber, U. (2019, January 19). Bayesian reasoning in nLab. Retrieved March 4, 2021, from https://ncatlab.org/nlab/show/Bayesian+reasoning
Donnat, C., & Holmes, S. (in press). Modeling the Heterogeneity in COVID-19’s Reproductive Number and its Impact on Predictive Scenarios. Cornell University.
Galesic, M., & Garcia-Retamero, R. (2010). Statistical Numeracy for Health. Archives of Internal Medicine, 170(5), 462–468. https://doi.org/10.1001/archinternmed.2009.481
Gigerenzer, G., & Hoffrage, U. (1995). How to improve Bayesian reasoning without instruction: Frequency formats. Psychological Review, 102(4), 684–704. https://doi.org/10.1037/0033-295x.102.4.684
Grupe, D. W., & Nitschke, J. B. (2013). Uncertainty and anticipation in anxiety: an integrated neurobiological and psychological perspective. Nature Reviews Neuroscience, 14(7), 488–501. https://doi.org/10.1038/nrn3524
Kurzenhäuser, S., & Hoffrage, U. (2002). Teaching Bayesian reasoning: an evaluation of a classroom tutorial for medical students. Medical Teacher, 24(5), 516–521. https://doi.org/10.1080/0142159021000012540
McCann, B. T. (2020). Using Bayesian Updating to Improve Decisions under Uncertainty. California Management Review, 63(1), 26–40. https://doi.org/10.1177/0008125620948264
Mcgrayne, S. B. (2012). The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines, and Emerged Triumphant from Two Centuries of Controversy (37310th ed.). New Haven, CT: Yale University Press.
Miller, A. B., Wall, C., Baines, C. J., Sun, P., To, T., & Narod, S. A. (2014). Twenty five year follow-up for breast cancer incidence and mortality of the Canadian National Breast Screening Study: randomised screening trial. BMJ, 348, g366. https://doi.org/10.1136/bmj.g366
Spiegelhalter, D., Pearson, M., & Short, I. (2011). Visualizing Uncertainty About the Future. Science, 333(6048), 1393–1400. https://doi.org/10.1126/science.1191181
Trimmer, P. C., Houston, A. I., Marshall, J. A. R., Mendl, M. T., Paul, E. S., & McNamara, J. M. (2011). Decision-making under uncertainty: biases and Bayesians. Animal Cognition, 14(4), 465–476. https://doi.org/10.1007/s10071-011-0387-4
Uehara, T., Yokomizo, H., & Iwasa, Y. (2005). Mate‐Choice Copying as Bayesian Decision Making. The American Naturalist, 165(3), 403–410. https://doi.org/10.1086/428301
Watkins, G. P., & Knight, F. H. (1922). Knight’s Risk, Uncertainty and Profit. The Quarterly Journal of Economics, 36(4), 682. https://doi.org/10.2307/1884757